Schuette–Nesbitt formula
In probability theory, the Schuette–Nesbitt formula is a generalization of the probabilistic version of the inclusion-exclusion principle. It is named after Donald R. Schuette and Cecil J. Nesbitt.
The Schuette–Nesbitt formula has practical applications in actuarial science, where it is used to calculate the net single premium for life annuities and life insurances based on the general symmetric status.
Contents |
Statement of the formula
Consider arbitrary events A1, ..., Am in a probability space 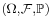 and let
and let
denote the random number of these events which occur simultaneously. Define
where the intersection over the empty index set is defined as Ω, hence S0 = 1.
Furthermore, consider the shift operator E and the difference operator Δ, which we define here on the sequence space of a real or complex vector space V by
and
Then
and, for every sequence c = (c0, c1, c2, c3, ..., cm, ...),
The quantity in (**) is the expected value of cN.
Remarks
- Normally, the name Schuette–Nesbitt formula refers to equation (**), where V denotes the set of real numbers.
- E0 and Δ0 denote the identity operator I on the sequence space, En and Δn denote the n-fold composition.
- In equation (**), (Δnc)0 denotes the 0th component of the sequence Δnc.
- The left-hand side of equation (*) is a convex combination of the powers of the shift operator E, it can be seen as the expected value of random operator EN. Accordingly, the left-hand side of equation (**) is the expected value of random component cN. Note that both have a discrete distribution, hence expectations are just the well-defined finite sums.
- The inclusion-exclusion principle can be derived from equation (**) by choosing the sequence c = (0,1,1,...): the left-hand side reduces to the probability of the event {N ≥ 1}, which is the union of A1, ..., Am, and the right-hand side is S1 – S2 + S3 – ... – (–1)mSm, because (Δ0c)0 = 0 and (Δnc)0 = –(–1)n for 1 ≤ n ≤ m.
- Equations (*) and (**) are also true when the shift operator and the difference operator are considered on a subspace like the ℓ p spaces.
- If desired, the formulae and the proof below can be considered in finite dimensions, because only the first m + 1 components of the sequences matter. Hence, represent the shift operator E and the difference opertor Δ as mappings of the (m + 1)-dimensional Euclidean space into itself, given by the (m + 1) × (m + 1)-matrices
-
- and let I denote the (m + 1)-dimensional identity matrix. Then (**) holds for every vector c = (c0, c1, ..., cm)T in (m + 1)-dimensional Euclidean space, where the exponent T in the definition of c denotes the transpose.
For textbook presentations of the Schuette–Nesbitt formula and their applications to actuarial science, cf. Gerber Life Insurance Mathematics, Chapter 8, or Bowers et al. Actuarial Mathematics, Chapter 18 and the Appendix, pp. 577–578.
History
For independent events, the formula appeared in 1959 in a discussion of Robert P. White and T.N.E. Greville's paper by Donald R. Schuette and Cecil J. Nesbitt in the Transactions of Society of Actuaries. In a two-page note appearing 1979, Hans U. Gerber called it Schuette–Nesbitt formula and generalized it to arbitrary events. In 1994, Christian Buchta published an elementary combinatorial proof; see the references below.
Cecil J. Nesbitt, PhD, F.S.A., M.A.A.A., received his mathematical education at the University of Toronto and the Institute for Advanced Study in Princeton. He taught actuarial mathematics at the University of Michigan from 1938 to 1980. He served the Society of Actuaries from 1985 to 1987 as Vice-President for Research and Studies. Professor Nesbitt died in 2001. (Short CV taken from Bowers et al., page xv.)
Donald Richard Schuette was a PhD student of C. Nesbitt, he later became professor at the University of Wisconsin–Madison.
The Schuette–Nesbitt formula (**) generalizes much older formulae of Waring, which express the probability of the events {N = k} and {N ≥ k} in terms of S1, S2, ..., Sm. More precisely, with 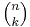 denoting the binomial coefficient,
denoting the binomial coefficient,
and
see Feller, Sections IV.3 and IV.5, respectively.
To see that these formulae are special cases of the Schuette–Nesbitt formula, note that by the binomial theorem
Applying this operator identity to the sequence c = (0, ..., 0, 1, 0, 0, ...) with k leading zeros and noting that (E jc)0 = 1 if j = k and (E jc)0 = 0 otherwise, the first formula for {N = k} follows from (**).
Applying the identity to c = (0, ..., 0, 1, 1, 1, ...) with k leading zeros and noting that (E jc)0 = 1 if j ≥ k and (E jc)0 = 0 otherwise, equation (**) implies that
Expanding (1 − 1)n using the binomial theorem and using equation (11) of the formulas involving binomial coefficients, we obtain
Hence, we have the formula for {N ≥ k}
Proof
The second equation (**) follows from the first one (*) by applying it to the sequence c and considering of the 0th component, because (Enc)0 = cn.
To prove (*), we first want to verify the operator equation
involving indicator functions of the events A1, ..., Am and their complements with respect to Ω. Suppose an ω from Ω belongs to exactly k events out of A1, ..., Am, where 0 ≤ k ≤ m, for simplicity of notation say that ω only belongs to A1, ..., Ak. Then the left-hand side is Ek. On the right-hand side, the first k factors equal E, the remaining ones equal the identity operator I, their product is also Ek, hence the formula is true.
Note that the difference operator Δ is the difference of the shift operator E and the identity operator I, meaning that Δ = E – I, hence
Inserting this result into the operator equation and expanding the product gives
because the product of indicator functions is the indicator function of the intersection.
Taking the expectation and using its linearity, we get (*).
An application in actuarial science
Problem: Suppose there are m persons aged x1, ..., xm with remaining random (but independent) lifetimes T1, ..., Tm. Suppose the group signs a life insurance contract which pays them after t years the amount cn if exactly n persons out of m are still alive after t years. How high is the expected payout of this insurance contract in t years?
Solution: Let Aj denote the event that person j survives t years, which means that Aj = {Tj > t}. In actuarial notation the probability of this event is denoted by 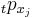 and can be taken from a life table. Use independence to calculate the probability of intersections. Calculate S1, ..., Sm and use the Schuette–Nesbitt formula (**) to calculate the expected value of cN.
and can be taken from a life table. Use independence to calculate the probability of intersections. Calculate S1, ..., Sm and use the Schuette–Nesbitt formula (**) to calculate the expected value of cN.
An application in probability theory
For a real number z set cn = zn for 0 ≤ n ≤ m. By the binomial theorem,
hence
Using the Schuette–Nesbitt formula (**), we get for the probability-generating function of N
Now let σ be a random permutation of the set {1,...,m} and let Aj denote the event that j is a fixed point of σ, meaning that Aj = {σ(j) = j}. When the numbers in J, which is a subset of {1,...,m}, are fixed points, then there are (m − |J|)! ways to permute the remaining m − |J| numbers, hence
By the combinatorical interpretation of the binomial coefficient, there are 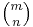 different choices of a subset J of {1,...,m} with n elements, hence
different choices of a subset J of {1,...,m} with n elements, hence
and
This is the partial sum of the infinite series giving the exponential function at z − 1, which in turn is the probability-generating function of the Poisson distribution with parameter 1. Therefore, as m tends to infinity, the distribution of N converges to the Poisson distribution with parameter 1.
See also
References
- Newton L. Bowers, Hans U. Gerber, James C. Hickman, Donald A. Jones, Cecil J. Nesbitt: Actuarial Mathematics. (2nd ed.), 1997, The Society of Actuaries ISBN 0-938959-46-8.
- Christian Buchta: An Elementary Proof of the Schuette–Nesbitt Formula. Mitteilungen der Schweiz. Vereinigung der Versicherungsmathematiker, Heft 2/1994, pages 219–220.
- William Feller: An Introduction to Probability Theory and Its Applications, Volume I. (3rd ed., revised printing), 1968, John Wiley & Sons. ISBN 0-471-25708-7.
- Hans U. Gerber: A Proof of the Schuette–Nesbitt Formula for Dependent Events. Actuarial Research Clearing House, 1979, Vol. 1. pages 9–10. Online
- Hans U. Gerber: Life Insurance Mathematics. (3rd ed.), 1997, Springer-Verlag, ISBN 3-54062-242-X.
- Donald R. Schuette and Cecil J. Nesbitt, Discussion of the preceding paper by Robert P. White and T.N.E. Greville, Transactions of Society of Actuaries, 1959, Vol. 11, No. 29AB, pages 97–99. Online
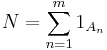
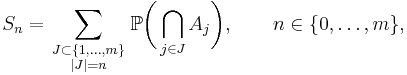
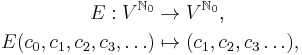
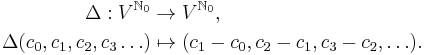
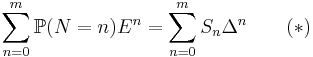
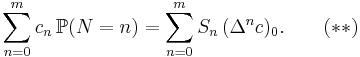
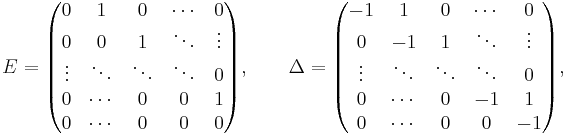
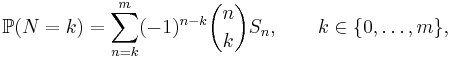
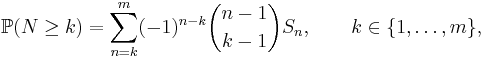
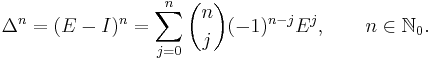
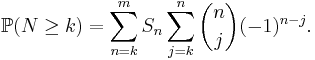
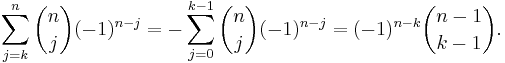
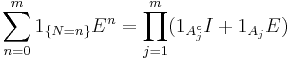
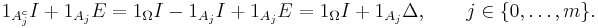
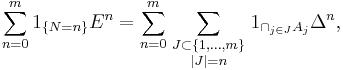
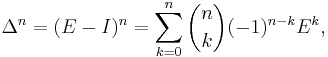
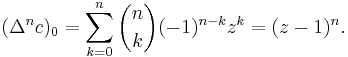
![\mathbb{E}[z^N]=\sum_{n=0}^m(z-1)^nS_n,\qquad z\in\mathbb{R}.](/2012-wikipedia_en_all_nopic_01_2012/I/94adb6e157ecc8ff146cfe6e2a87ed4f.png)
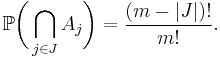
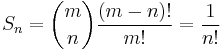
![\mathbb{E}[z^N]=\sum_{n=0}^m\frac{(z-1)^n}{n!},\qquad z\in\mathbb{R}.](/2012-wikipedia_en_all_nopic_01_2012/I/f581cb3ed3c98b797748b03553f16d32.png)